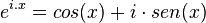Potências e suas propriedades

domingo, 24 de maio de 2009

quinta-feira, 21 de maio de 2009

Expoentes irracionais

expoentes próximos geram resultados próximos , pode-se definir expoentes irracionais:

$x^\pi \approx x^{3.14159}\,$

Expoentes imaginários e complexos

considera-se que:

$e^{i.x} = cos (x) + i \cdot sen (x)$

usando logaritmos, podemos definir para qualquer a real e z complexo, z = x + i y:

$a^z = (e^{\log a})^z = e^{(z \cdot \log a)} = a^x \ (cos(y \ \log a) + i \cdot sen(y \ \log a))\,$

segunda-feira, 18 de maio de 2009

Material Dourado

Mateiral Dourado ou Montessori possui vários cubinhos, barras, placas e cubão:

o cubo é formado por 10 placas, que a placa é formada por 10 barras e representam centena e a barra representa dezena e um cubinho é a unidade

Veja como representamos, com ele, o número 265:

Este material é feito em madeira, costuma ser comercializado com o nome de material dourado. Você pode construir um material semelhante, usando cartolina.

Embora seja possível representar o milhar, vamos evitá-lo trabalhando com números menores.

Damos a seguir sugestões para o uso do Material Dourado Montessori.

O professor saberá em que série cada atividade poderá ser aplicada com melhor rendimento. Várias das atividades podem ser aplicadas em mais de uma série, bastando, para isso, pequenas modificações.

Quadrados e cubos

Elevar potência 2 chama-se elevar ao quadrado. Por exemplo, 3² = 9.

Os números 1, 4, 9, 16, 25 etc. também são conhecidos como quadrados perfeitos ou números quadrados.
podemos representar todos esses números em grades formando quadrados.

Elevar à terceira potência chama-se também elevar ao cubo.

Os cubos ou números cúbicos são os que resultam de se elevarem números naturais à potência 3, pois nos remetem ao volume de um cubo. São cubos 1, 8, 27, 64, 125 etc., porque são o resultado de 1³, 2³, 3³, 4³, 5³.

veja mais em: http://www.klickeducacao.com.br/2006/materia/20/display/0,5912,POR-20-86-956-,00.html

Potenciação de números racionais

O expoente é um número maior ou igual a 11:

* se o expoente é um par, a potência é positiva
* se o expoente é um número impar, o sinal de potência é o mesmo da base
* se o expoente é 1, a potência é igual à própia base

O expoente é igual a zero:

*qualquer número diferente de zero e dividido por ele mesmo dá 1
*qualquer número elevado a zero é 1

O expoente é um número inteiro positivo:

Se a é número real e n é inteiro e positivo, a expressão aⁿ representa o produto de n fatores todos iguais a "a".

Na expressão aⁿ, o número real a é denominado base e n é denominado expoente

Exemplos

2³=2 . 2 . 2 = 8

(-4)² = (-4) . (-4) = 16

(-5)³ = (-5) .(-5) . (-5) = -125

Para n=1, define=se a¹ = a

10¹ = 10

Potências de base 10 com expoente inteiro negativo

Potências de base 10 resultam da multiplicação de vários números 10.portanto,sempre equivalerão à unidade seguida de tantos zeros quantos forem os indicados pelo expoente natural.

Potência de base 10

Um número multiplicado por uma potência de base 10 positiva, indica que iremos "aumentar" o número de zeros à direita ou "movimentar" para direita a vírgula tantas casas quanto indicar o expoente da base 10. Veja alguns exemplos:

54 x 10⁵	=	5400000	Acrescentamos 5 zeros à direita do 54
2050 x 10²	=	205000	Acrescentamos 2 zeros à direita do 2050
0,00021 x 10⁴	=	2,1	"Movimentamos" a vírgula 4 casas para direita
0,000032 x 10³	=	0,032	"Movimentamos" a vírgula 3 casas para direita

Quando temos um número multiplicado por uma potência de base 10 negativa, indica que iremos "diminuir" o número de zeros à direita ou "movimentar" a vírgula para esquerda tantas casas quanto indicar o expoente da base 10. Veja alguns exemplos:

54 x 10^-5	=	0,00054	"Movimentamos" a vírgula 5 casas para esquerda
2050 x 10^-2	=	20,5	"Movimentamos" a vírgula 2 casas para esquerda. Lembrando que 20,5 = 20,50
0,00021 x 10^-4	=	0,000000021	"Movimentamos" a vírgula 4 casas para esquerda
0,000032 x 10^-3	=	0,000000032	"Movimentamos" a vírgula 3 casas para esquerda
32500000 x 10^-4	=	3250	"Diminuimos" 4 zeros que estavam à direita

Fonte:http://www.tutorbrasil.com.br/estudo_matematica_online/algebra_basica/algebra_basica_03_potencia_base_10.php

exercicio resolvido

O número de elementos distintos da sequência 2⁴, 4², 4^-2 (-4)², (-2)⁴, (-2)^-4 é:

a) 8
b) 2
c) 7
d) 9

Solução:

Para determinar o número de elementos distintos é suficiente que calculemos cada um deles. Assim temos:

2⁴ = 2 x 2 x 2 x 2 = 16
4² = 4 x 4 = 16
4^-2 = 1/ 4² = 1/16 (uso da propriedade e) do artigo sobre potenciação)
(-4)² = (-4) x (-4) = 16 (potência par de base negativa tem como resultado um número positivo)
(-2)⁴ = (-2) x (-2) x (-2) x (-2) = 16 (idem)
(-2)^-4 = 1/(-2)⁴ = 1/16 (uso da propriedade e) do artigo sobre potenciação)

Portanto, se conclui que existem dois elementos distintos (16 e 1/16) e a resposta correta é a b).

domingo, 24 de maio de 2009

video sobre potencias